Pour mesurer un objet, comme un cratère lunaire ou un diamètre d’un objet céleste à partir d’une image, il est nécessaire d’utiliser une référence de taille connue dans la même image. Par exemple, si vous avez une image d’un cratère lunaire et que vous voulez mesurer son diamètre, vous pouvez trouver un autre cratère à proximité dont le diamètre est connu et utiliser cela comme référence.
Ensuite, vous pouvez utiliser un logiciel d’édition d’images pour mesurer la distance en pixels entre les deux objets (Photoshop, ImageJ, Pixinsight…) et convertir cette distance en une distance physique en utilisant la référence de taille connue. Pour ce faire, il faut connaître la résolution de l’image, c’est-à-dire le nombre de pixels par unité de longueur.
Une autre option consiste à utiliser un logiciel de traitement d’images spécialisé dans l’analyse astronomique, qui peut automatiquement mesurer les dimensions des objets célestes à partir d’images en utilisant des algorithmes de reconnaissance d’objets. Il est important de noter que la précision des mesures dépendra de la qualité de l’image, de la résolution, de la méthode utilisée et des erreurs potentielles associées à chaque étape du processus.

Les choses que vous devez savoir :
- Longueur focale de votre télescope (Ou téléobjectif)
- Taille du pixel de la camera
Dans mon cas, la longueur focale de mon téléobjectif est d’environ 600 mm. La caméra que j’utilise est la caméra Nikon D850 qui a une taille de pixel de 4,35um,
On commence par mesurer l´objet sous Photoshop en utilisant l´outil règle,
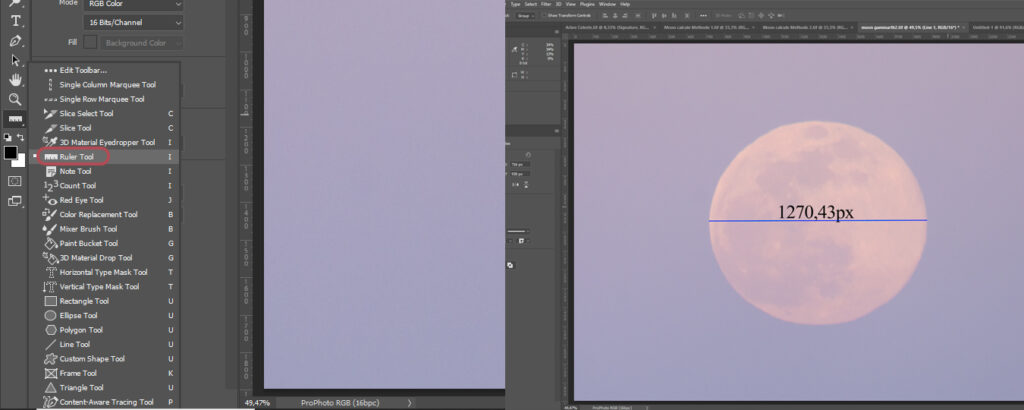
Maintenant on va passer aux calculs par échantillonnage
Rappel :
L’échantillonnage d’un télescope est une mesure de la résolution angulaire du télescope. Cela correspond à la capacité du télescope à séparer les détails fins d’un objet observé. Plus l’échantillonnage est fin, meilleure est la résolution angulaire.
L’échantillonnage dépend de la taille de l’ouverture du télescope (diamètre de l’objectif ou du miroir), de la longueur focale de l’objectif ou du miroir et de la taille des pixels de la caméra utilisée pour l’observation.
Lorsque l’échantillonnage est trop fin, la taille des pixels de la caméra est plus petite que la résolution limite du télescope, ce qui signifie que l’observation n’est pas optimale et que la résolution angulaire n’est pas utilisée de manière efficace. D’autre part, si l’échantillonnage est trop grossier, la résolution angulaire ne peut pas être suffisamment exploitée, ce qui entraîne une perte de détails fins dans l’observation.
Formule :
Cette formule permet de calculer la taille angulaire d’un pixel d’une image prise par un télescope, en fonction de la taille des pixels de la caméra utilisée et de la longueur focale de l’objectif ou du miroir du télescope. La taille angulaire est exprimée en arcsecondes.
E = (Taille pixel / longueur focale) * 206.265
Où :
- E est la taille angulaire d’un pixel en arcsecondes
- Taille pixel est la taille physique d’un pixel sur le capteur de la caméra, exprimée en microns
- Longueur focale est la longueur focale de l’objectif ou du miroir du télescope, exprimée en millimètres.
La constante 206,265 est utilisée pour convertir la valeur obtenue en degrés en arcsecondes.
Cette formule est utile pour déterminer la résolution angulaire d’un télescope en utilisant les caractéristiques de la caméra utilisée pour l’observation. Elle permet également de déterminer la taille des objets célestes ou la taille des détails fins d’un objet observé.
Pour rappel : 1 degrés = 60 min d’arc = 3600 secondes d’arc.
E= (4,35/600)*206,265 = 1,4954 arcsec par pixel
Cela signifie que chaque pixel de l’image prise par votre télescope a une taille angulaire de 1,4954 arcsecondes. Cette information peut être utile pour déterminer la résolution angulaire de votre télescope et pour choisir les objets célestes à observer en fonction de leur taille apparente.
Alors la longueur en arcsec du diamètre de la Lune serait de :
1270,43 pixels * 1,4954 arcsec/pixel = 1899,828 arcsec
Donc, si la longueur en pixel du diamètre de la Lune est de 1270,43 pixels, alors le diamètre de la Lune mesure environ 1899,828 arcsec en taille angulaire.

Le diamètre de la Lune en kilomètres peut être calculé en utilisant la formule suivante :
Diamètre de la Lune (en km) = Taille angulaire de la Lune (en arcsec) * Distance de la Lune (en km) / 206265
Dans ce cas, si la distance de la Lune au moment de la prise de vue était de 406050 km et que la taille angulaire de la Lune était de 1899,828 arcsec, nous pouvons calculer le diamètre de la Lune en kilomètres en utilisant la formule suivante :
Diamètre de la Lune (en km) = Taille angulaire de la Lune (en arcsec) * Distance de la Lune (en km) / 206265
En remplaçant les valeurs, nous avons :
Diamètre de la Lune (en km) = 1899,828 * 406050 / 206265 = 3740 km (environ)
Ainsi, avec cette distance de 406050 km et une taille angulaire de 1899,828 arcsec, le diamètre de la Lune serait d’environ 3740 km.
Cette méthode peut être utilisée pour mesurer la taille angulaire de n’importe quel objet céleste, pourvu que nous connaissions la distance de l’objet par rapport à nous et que nous ayons une mesure précise de sa taille angulaire en arcsec.
Cependant, il convient de noter que cette méthode est basée sur des approximations et des modèles simplifiés de la géométrie de l’objet céleste et de la manière dont la lumière est captée par notre télescope et notre caméra. Il peut y avoir des erreurs dues à des facteurs tels que la turbulence atmosphérique, les effets de diffraction, la résolution de l’instrument et la qualité de la mise au point, qui peuvent affecter la précision de la mesure.
Il est donc important d’utiliser cette méthode avec prudence et de prendre en compte toutes les sources d’erreur possibles lors de l’analyse des résultats obtenus.

D’autres méthodes pour mesurer la taille et les distances des objets célestes. En voici quelques-unes :
- Parallaxe : cette méthode est utilisée pour mesurer les distances des étoiles proches. Elle consiste à mesurer l’angle que fait la position apparente de l’étoile avec deux positions d’observation différentes, distantes d’une certaine distance connue. La différence entre ces deux positions angulaires permet de calculer la distance de l’étoile.
- Spectroscopie : cette méthode est utilisée pour mesurer la vitesse et la distance des étoiles, des galaxies et d’autres objets célestes en utilisant l’analyse de la lumière qu’ils émettent. La mesure du décalage Doppler de la lumière permet de déterminer la vitesse radiale de l’objet, qui est ensuite utilisée pour calculer sa distance.
- Méthode des bougies standard : cette méthode est utilisée pour mesurer les distances cosmiques en utilisant des objets célestes de luminosité connue, tels que les supernovae de type Ia. La relation entre la luminosité de l’objet et sa distance est utilisée pour calculer les distances d’autres objets similaires.
- Astrométrie : cette méthode consiste à mesurer la position et le mouvement des objets célestes dans le ciel en utilisant des télescopes et des caméras précises. La mesure précise de la position et du mouvement peut être utilisée pour calculer la distance et la taille des objets.
Il existe de nombreuses autres méthodes utilisées en astronomie pour mesurer les propriétés des objets célestes, en fonction des caractéristiques de l’objet et des instruments disponibles.
© 2023 Makrem Larnaout
Pour la maintenance de votre télescope Cliquer Ici
N‘oubliez pas de consulter notre rubrique Formation Télescope



